Are Machines Better at Designing Practice Problems than Humans ?

Visuals are used in subjects like science, technology, engineering, and math (STEM). For example, chemistry lessons on bonding typically includes the visuals shown in Figure 1. While we usually assume that these visuals help students learn because they make abstract concepts clearer, they can also harm students’ learning if students do not know how the visuals show information. To learn from visuals, students need representational competencies — knowledge about how visual representations show information. For example, a chemistry student needs to learn that the dots in the Lewis structure (Figure 1a) show electrons and that the spheres in the space-filling model (Figure 1b) show areas where electrons may live.

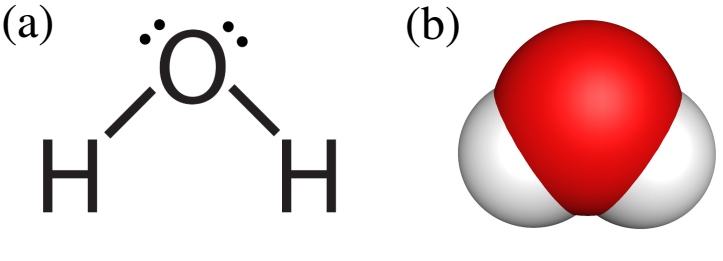
Figure 1: Two common visual representations of water (a: Lewis structure; b: space-filling model).

Lessons that help students learn representational competencies mostly focuse on conceptual representational competencies. These include the ability to connect visual features to concepts, support conceptual reasoning with visuals, and choose the right visuals to illustrate a given concept. Less research has focused on a second type of representational competency — perceptual fluency. This is the ability to quickly and effortlessly see meaningful information in visuals. For example, chemists can effortlessly see that both visuals in Figure 1 show water. Perceptual fluency plays an important role in students’ learning because it frees mental energy for more complex reasoning. This allows students to learn from visuals.

Students get perceptual fluency through learning processes that are implicit and inductive. To understand this, think about the the way you learned your first language. You didn't need to effortfully think about the grammatical rules. Instead, you got a "feel" for the rules (implicit learning) that came from many learning opportunities (inducing process). Because of this, it is thought that perceptual fluency should be taught by giving students many simple tasks in which they must quickly judge what a visual shows. For example, a perceptual fluency task may ask students to quickly and intuitively judge whether two visuals like the ones in Figure 1 show the same molecule. They ask students to rely on implicit intuitions. The problem sequence is typically chosen so that (1) students are exposed to a variety of visuals and (2) consecutive visuals vary irrelevant features while drawing attention to relevant features.

However, these general guidelines leave many possible sequences open. So far, we do not have a principle-based way of identifying the best problem sequences. In our study, we used a created a computer model of how undergraduates learn to solve perceptual fluency problems in chemistry. Then, we had a computer algorithm teach the first model. Finally, we took the problem sequence that worked best for the model and gave it to real humans on the Internet. We found that the sequence of chemistry visuals (practice problems) created by the machine was better for learning than a random problem sequence and a sequence generated by a human expert who knew about chemistry and perceptual learning.

Perceptual Fluency

Representations used when teaching are defined as external representations because they are external or outside of the viewer. By contrast, internal representations are mental objects that students can imagine and mentally manipulate. External representations can be symbolic like the text in a book or visual like Lewis structures in chemistry.

Perceptual fluency research is based on findings that experts like doctors and pilots can automatically see meaningful connections among representations, that it takes them little cognitive effort to translate among representations, and that they can quickly and effortlessly mix information distributed across representations. For example, chemists can see at a glance that the Lewis structure in Figure 1A shows the same molecule as the space-filling model in Figure 1B. This kind of perceptual expertise frees up cognitive resources for more complex reasoning.

According to two learning theories, perceptual fluency involves building accurate internal representations of visuals and connecting them to each other.

Cognitive science suggests that students get perceptual fluency by perceptual induction processes. Here, inductive means that students can figure out how visual properties relate to concepts through practice. Students become better at seeing meaning in visuals by treating each visual feature property as one perceptual chunk that relates to multiple concepts (perceptual chunking). Perceptual induction processes are thought to be nonverbal happen unconsciously.

Lessons that target perceptual fluency are fairly new. Some researchers have created math and science lessons in which students translate between different visuals quickly. In our chemistry study, students judged whether two visuals like the ones shown in Figure 1 show the same molecule. Students would get dozens of problems like these in a row. These interventions can raise test scores even if the problems are a bit different from the problems used during the lesson.

Perceptual learning depends on the practice sequence. To design good sequences, tasks should give students a variety of problems so that irrelevant features vary but relevant features are constant across several tasks. But we know that visuals differ from each other in many ways. So there are many possible sequences that could vary visual features. To address this problem, we used a new computer science approach called maching teaching.

Machine Teaching Procedure

Machine teaching is a computer science technique in which a computer algorithm helps improve human learning. We took the following steps:

1. In a learning experiment, we ran an experiment to figure out how real human students relate different visuals like the two molecules above (Figure 1).
2. From that data, we created a cognitive model of chemistry visual learning. This model was a step-by-step problem-solving procedure called an algorithm.
3. We used an algorithm to find an optimal machine-generated problem sequence.
4. The machine-generated sequence was used to teach the cognitive model and predict learning.
5. On the Internet, we tested all three sequences (machine, human expert, random) with actual humans.

Which problem sequence is best for learning? We wondered whether an algorithm run by a machine could improve learning beyond a random problem sequence and a sequence created by a human expert.

Step 1: How do Humans Learn to Map Visuals?

First, we needed to train a learning algorithm that behaved like real humans on perceptual learning lessons. To do that, we ran a small experiment. We compared the learning algorithm’s predictions to humans' test scores. In our pilot experiment, we recruited 47 undergraduate chemistry students. They were randomly assigned to two conditions using random problem sequences -- training with feedback or training without feedback.

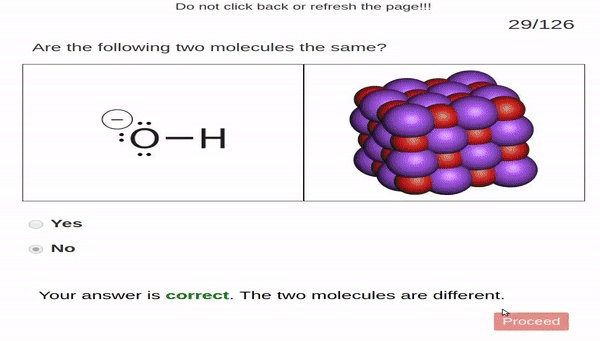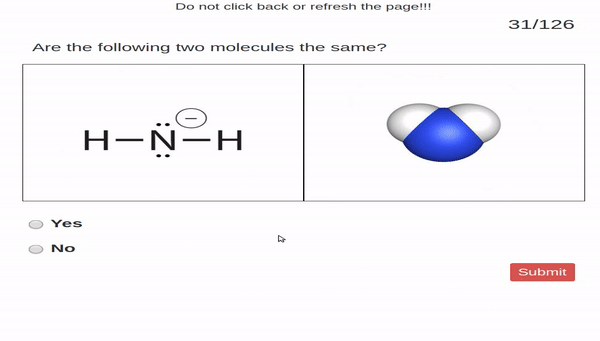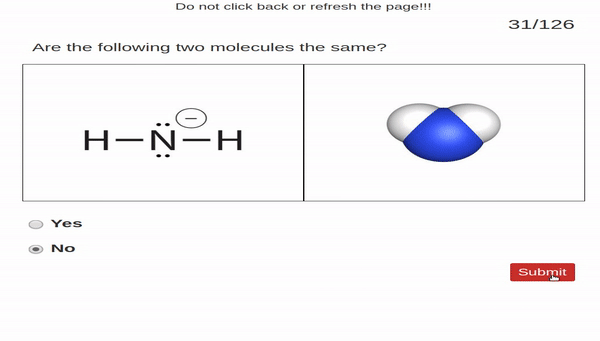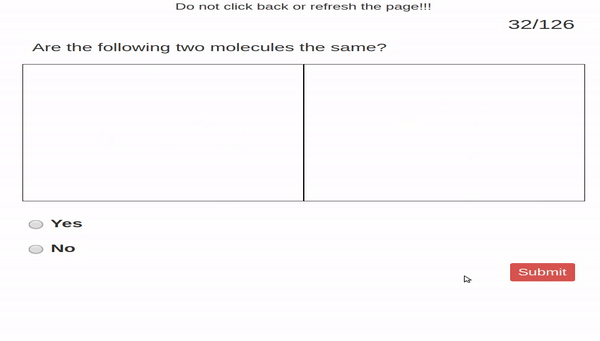
Perceptual fluency problems ask students to make simple perceptual judgments. In our case, students were given two images. One image was of a molecule represented by a Lewis structure and the other image was a molecule represented by a space-filling model. Students judged whether or not the two images show the same molecule.

Step 2: Cognitive Model of Human Learning

Now, we describe how we created the cognitive model of how humans learn with chemistry visuals. To do this, we describe the:

• perceptual fluency tasks and how we represent them precisely
• learning algorithm used by the cognitive model of human learning

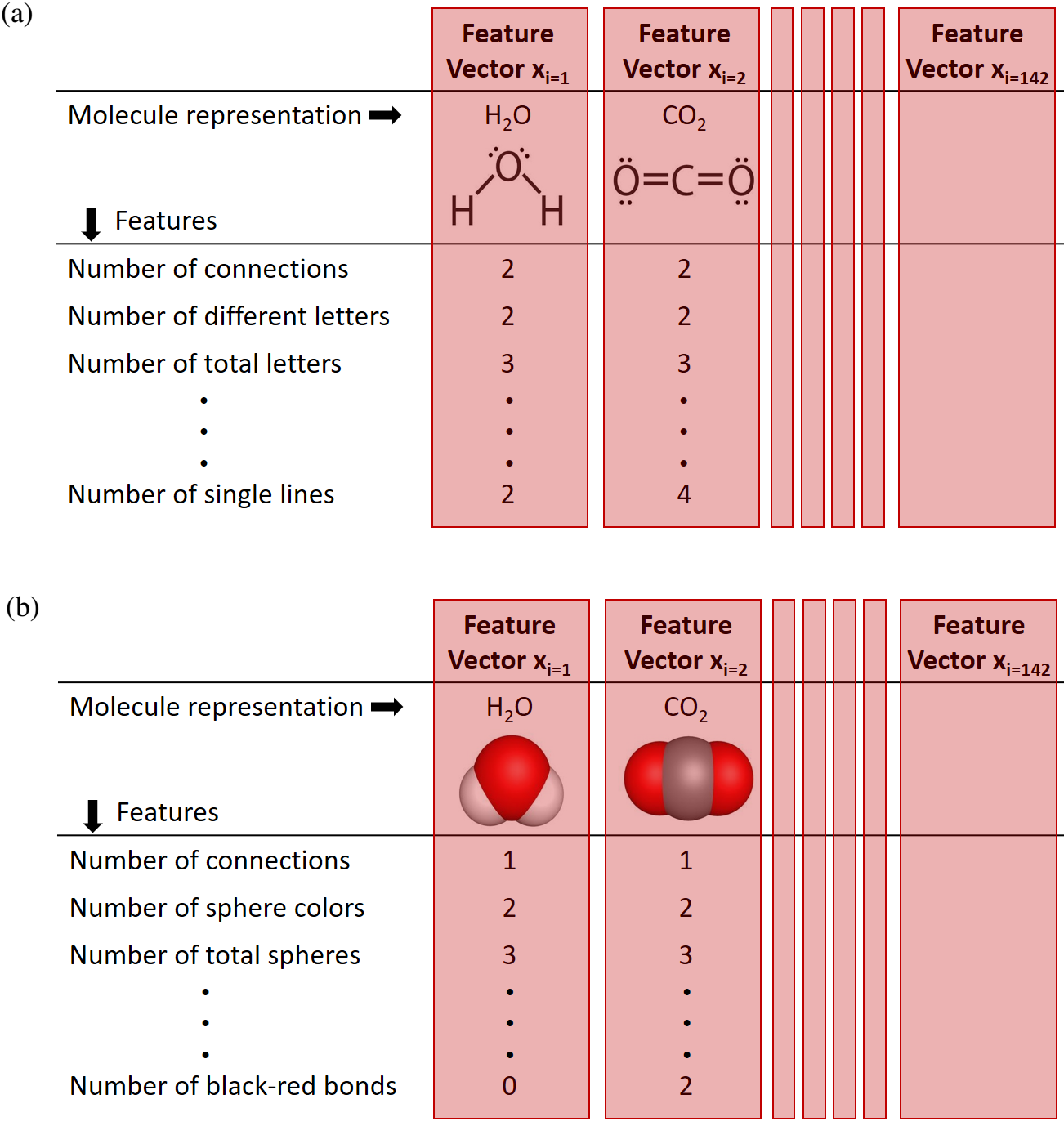
A - Describing Molecules to Computers

In our experiment, we used visual representations of chemical molecules common in undergraduate classes. To find these molecules, we reviewed textbooks and web-based content. We listed the frequency of different molecules using their chemical names (e.g., H2O) and chose the 142 most common molecules. To precisely describe the visual representations, we counted visual features like the number of lines or dots in the Lewis structure and the colors of spheres in the space-filling models. This allowed us to create lists of visual properties called feature vectors. Each molecule had a feature vector that described its visual features Feature vectors of Lewis structures had 27 features. Feature vectors of space-filling models had 24 features. These feature vectors were used by the learning algorithm.



B - A Learning Algorithm Behaving Like Humans

Our learning algorithm plugged in the two molecules (Lewis structure and space-filling model) as inputs in the form of feature vectors. It was important to represent the molecules as feature vectors because this translates the visual information to a "language" that software can understand.

Given these feature vectors as inputs, the learning algorithm was able to place them in the same "world". This world is the golden vector space. It can be thought of as a coordinate plane similar to the one in which you would place the points (0,4) and (9,3). Just as the distance between two points in a coordinate plane can be calculated using the distance formula, the distance between two molecules can also be calculated. The distance between two molecules represents their similarity. Two similar molecules will be very close together in the golden vector space and two dissimilar molecules will be far apart. Next, we calculate the probability that the two molecules were the same. When given the correct answer, the algorithm updated itself. Over many opportunities, this allows the algorithm to learn.

Step 3: Find the Best Problem Sequence

Our first problem was to consider the length of the problem sequences. Should we create sequences of 50 problems? Or 100? Searching over all possible sequences would be too complex for most computers. We settled on 60 as the length of the problem sequence because this was closest to other studies.

Finding the best problem sequence was a computationally tough problem. For each problem in the 60-problem sequence, there could be 5,041 possible options. This means that there were 5041⁶⁰ or 1.4 * 10²²² possible sequences. We can not hope to find the "best" or optimal sequence. So we settle for a sup-optimal or "good enough" sequence.

The algorithm that searchs for a suboptimal solution is called a modified hill climbining algorithm. We consider a landscape with different training sets scattered about. We begin by looking at a random random set and checking its neighbors. If the neighboring problem sequences result in better learning for the cognitive model, we move to the better training set.

Step 4: Teaching the Best Problem Sequence to the Cognitive Model

We continued this process until no better neighbors are found. Because of computer limits, we only checked 500 neighbors of a particular training set. The problem sequence that remained was our solution -- the machine-generated problem sequence.

Step 5: Testing All Three Sequences in a Human Internet Experiment

To find out whether the machine problem sequence is best for learning, we ran a randomized experiment with humans on the Internet.

Participants

We recruited 368 participants using Amazon’s Mechanical Turk (MTurk). Of these, 216 were male and 131 were female. The rest did not report their sex. Most participants (86%) were below the age of 45.

Experimental Design

We compared three training conditions. In the machine training sequence condition, we used the problem sequence found by the search algorithm.

---

Participants judged whether the two molecules were the same and received feedback. In the condition using the human expert sequence, the training set was constructed by an expert in perceptual learning and chemistry.

---

---

In the random training sequence condition, each problem was randomly created.

---



Procedure

We hosted the experiment online. Participants first received a brief description of the study and then completed a sequence of 126 judgment problems (yes or no). Tasks were divided into three phases. Phase one was the pretest and it included 20 test problems without feedback. Phase two was for training and it included 60 training problems with correctness feedback. We assumed that participants learned during this phase. Phase three was the posttest with 40 test problems displayed without feedback.

In addition, one guard task was inserted after every 19 tasks throughout all three phases. A guard question either showed two perfectly identical molecules shown by the same representation or two highly dissimilar molecules shown by Lewis structures. We used these easy guard questions to filter out participants who randomly clicked through the tasks. We ignored the guard tasks during modeling. When the images of the two molecules were shown to participants, the position (left or right) was randomized so that no representation was on one side more often.

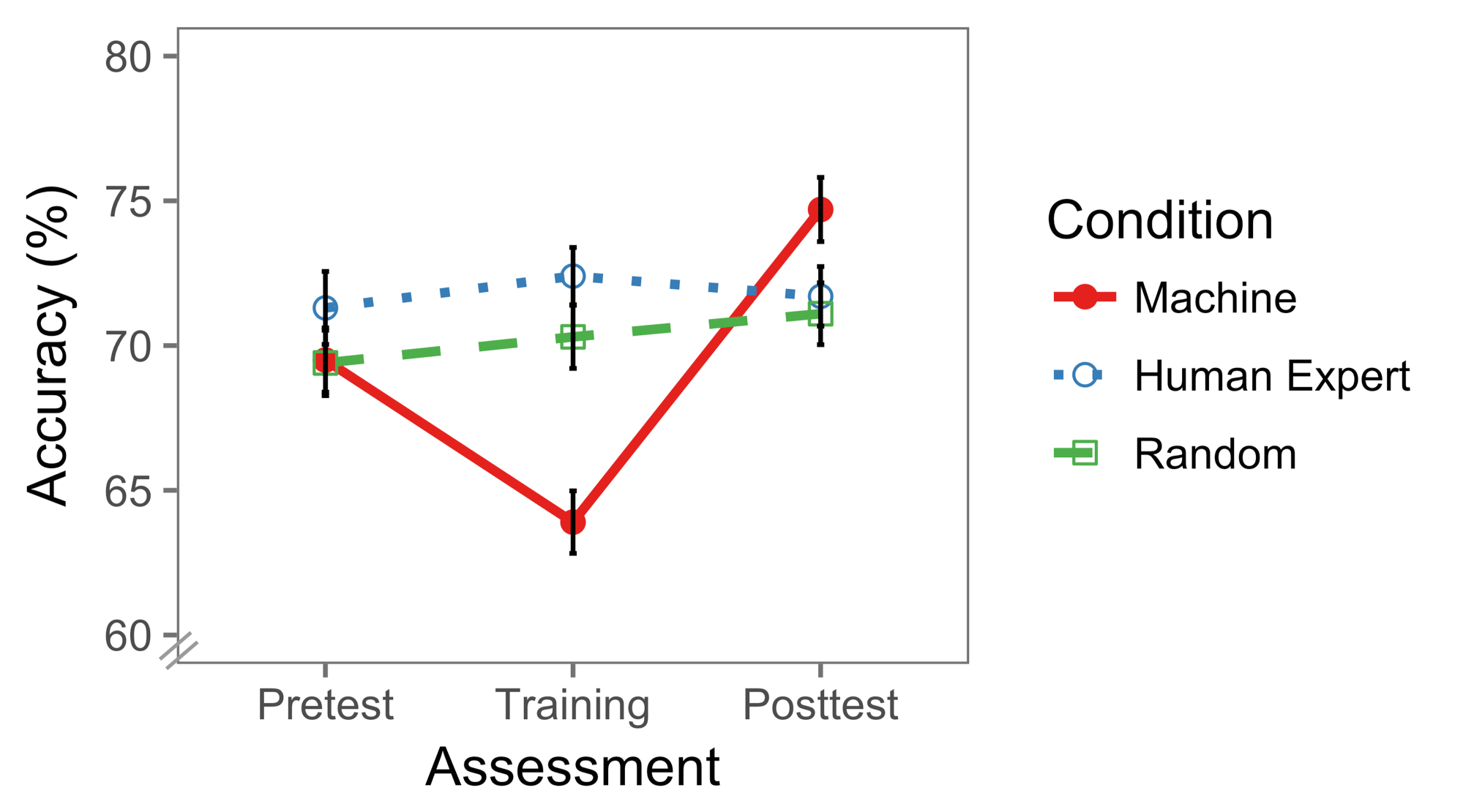
Results

Of the 368 participants, we filtered out 43 participants who failed any of the guard questions. The final sample size was 325. The final number of participants in the conditions random, human, and machine training sequence were 108, 117 and 100 respectively.

---



---

Conclusion

Our goal was to determine whether machine learning can help find a sequence of visual representations that raises students’ learning from perceptual-fluency tasks. To do this, we used machine teaching to reverse-engineer an optimal training sequence for a machine-learning algorithm. Next, we conducted an experiment with humans that compared the machine teaching sequence to a random sequence and to a sequence generated by a human expert on perceptual learning. The machine teaching sequence resulted in lower training performance, but higher posttest scores. The fact that the machine learning sequence yielded lower performance during training, but higher posttest scores suggests that this sequence induced desirable difficulties. Desirable difficulties refers to interventions yielding lower performance during training, but higher long-term learning. Given that visual representations are so common, we think that our findings will be broadly useful.